编辑工具：IDLE/Sublime Text

项目管理：pycharm/Anconada

第一章：python基本语法元素

1.1 程序设计基本方法

计算机是根据指令操作数据的设备，必须满足功能性（对数据的操作）和可编程性。

编程语言的执行方式分为编译和解释

编译;将源代码一次性转化为目标代码的过程

解释：将源代码逐条转换成目标代码同时逐条运行的过程

编程语言分为两类

静态语言：编译执行，c/c++/java

脚本语言：解释执行，Python/javaScript/PHP

1.2 Python开发环境配置

下载andaconda

汉化https://www.py.cn/tools/spyder/16379.html

更新conda

打开anaconda prompt
更新Anaconda，命令如下：
1
conda update conda
更新各种常用包，命令如下：
1
conda update --all
升级spyder命令为
1
conda update spyder

1.3 温度转换实例

#TempConvert.py
TempStr = input("请输入带有符号的温度值：")
if TempStr[-1] in ['F','f']
	C = (eval(TempStr[0:-1]) - 32)/1.8 #注意他是怎么取到字符串中所有的量
    print("转换后的温度是{:.2f}C".format(F))
elif TempStr[-1] in ['C','c']:
    F = 1.8*eval(TempStr[0:-1]) + 32
    print("转换后的温度是{:.2f}F".format(F))
else:
    print("输入格式错误")

1.4 Python程序语法元素分析

程序的格式框架

缩进：一行py代码开始前的空白区域，表达程序的格式框架(严格/所属/长度)

注释：用于提高代码可读性的辅助性文字，不被执行

命名与保留字

变量: 程序中用于保存和表示数据的占位符号

命名: 关联标识符的过程

命名规则 : 大小写字母、数字、下划线和中文等字符及组合

保留字: 被编程语言内部定义并保留使用的标识符

数据类型

数据类型: 供计算机程序理解的数据形式

数据类型：字符串、整数、浮点数、列表

字符串: 由 0 个或多个字符组成的有序字符序列

字符串由一对单引号或一对双引号表示
字符串是字符的有序序列，可以对其中的字符进行索引
字符串的序号: 正向递增序号和反向递减序号
字符串的使用: [ ]获取字符串中一个或多个字符
- 索引：返回字符串中单个字符 <字符串 >[]
- 切片：返回字符串中一段字符子串 <字符串 >[M: N]

数字类型: 整数和浮点数

列表类型: 由 0 个或多个数据组成的有序序列

列表使用 [ ]表示，采用逗号 (,)分隔各元素
使用保留字 in 判断一个元素是否在列表中

语句与函数

赋值语句：由赋值符号构成的一行代码

分支语句：由判断条件决定程序运行方向的语句

函数: 根据输入参数产生不同输出的功能过程

Python 程序的输入输出

输入函数input(): 从控制台获得用户输入的函数

使用格式：<变量 > input 提示信息字符串
用户输入的信息以字符串类型保存在<变量> 中

输出函数print(): 以字符形式向控制台输出结果的函数

print(<拟输出字符串或字符串变量>)
字符串类型的一对引号仅在程序内部使用，输出无引号
输出函数的格式化： print（转换后的温度是 {:.2f} C”. format(c))

eval()：去掉参数最外侧引号并执行余下语句的函数

eval(<拟输出字符串或字符串变量>)
理解执行余下语句是什么意思，数值会变成数值，运算符会参与运算

format()：函数控制输出格式

和%用法相似，

print(‘{}{}’).format(a,b)

print(‘{:.2f}b’).format(a)

第一章作业

n=input()
s="零一二三四五六七八九"
for c in "0123456789":
    n=n.replace(c,s[eval(c)]) #这行代码给我整懵了
print(n) 

通过作业理解字符串/字符数组的下标取用
TempStr = input()
print(TempStr[0])
>>F32
>>F

python与c语言是不同的，c语言中最后一位是\0

#TempConvert.py
TempStr = input()
if TempStr[0] == 'R':
    USD = eval(TempStr[3:])/6.78
    print("USD{:.2f}".format(USD))
elif TempStr[0] == 'U':
    RMB = 6.78*eval(TempStr[3:])
    print("RMB{:.2f}".format(RMB))

第二章：python基本图像绘制

2.1理解python语言

编程语言	学习内容	语言本质	解决问题	适用专业
C	指针、内存、数据类型	理解计算机系统结构	性能	计算机
Java	对象、跨平台、运行时	理解主客体关系	跨平台	软件
C++	对象、多态、继承	理解主客体关系	大规模程序	计算机
Python	编程逻辑、第三方库	理解问题求解	各类问题	所有

2.2绘制蟒蛇

#PythonDraw.py
import turtle
turtle.setup(650, 350, 200, 200)
turtle.penup()
turtle.fd(-250) 
turtle.pendown() 
turtle.pensize(25)
turtle.pencolor("purple")
turtle.seth(-40)
for i in range(4):
    turtle.circle(40, 80)
    turtle.circle(-40, 80)
turtle.circle(40, 80/2)
turtle.fd(40)
turtle.circle(16, 180)
turtle.fd(40 * 2/3)
turtle.done()

import+保留字

引入了一个绘图库

程序参数的改变

Python蟒蛇的颜色：黑色、白色、七彩色…

Python蟒蛇的长度：1节、3节、10节…

Python蟒蛇的方向：向左走、斜着走…

计算问题的扩展

Python蟒蛇绘制问题是各类图像绘制问题的代表

圆形绘制、五角星绘制、国旗绘制、机器猫绘制…

掌握绘制一条线的方法，就可以绘制整个世界

2.3第一个模块：turtle 库的使用

turtle 库基本介绍

Python计算生态 = 标准库 + 第三方库

标准库：随解释器直接安装到操作系统中的功能模块

第三方库：需要经过安装才能使用的功能模块

库Library、包Package、模块Module，统称模块

turtle 绘图窗体布局

turtle的一个画布空间中最小单位是像素

turtle的绘图窗体

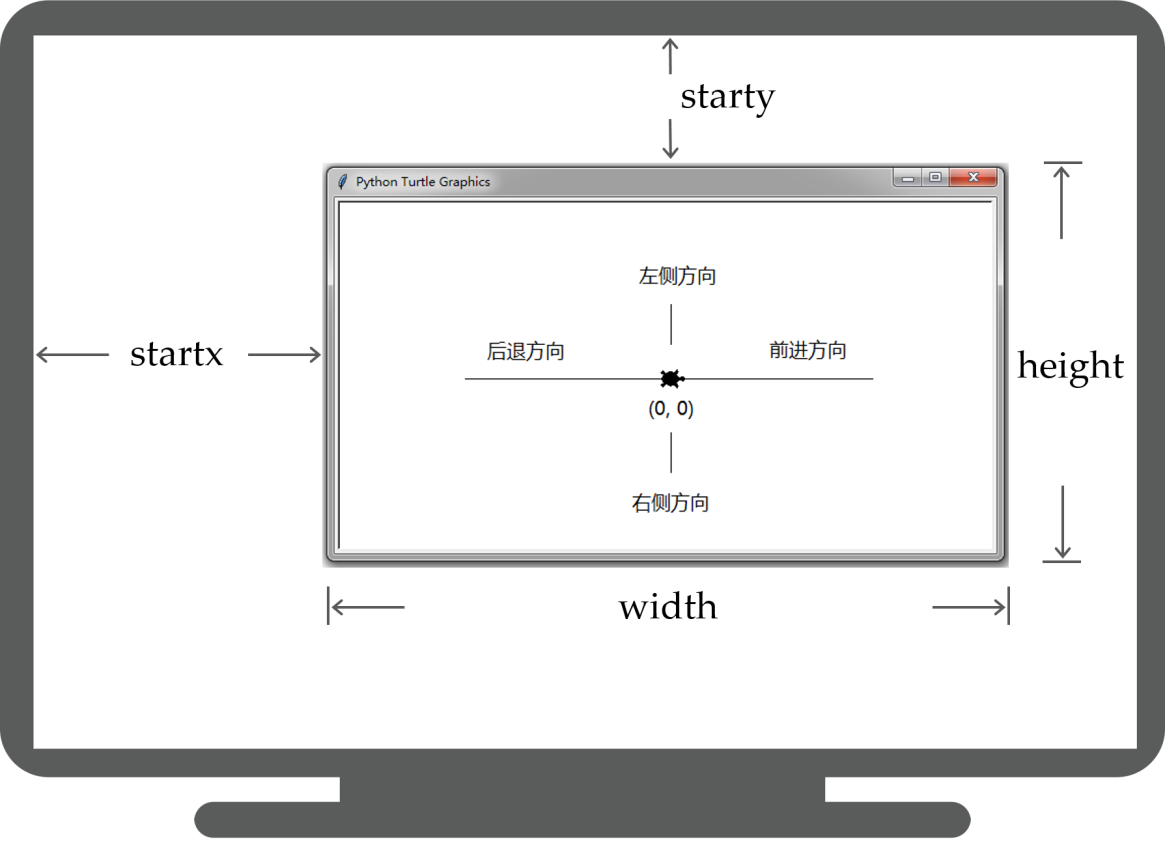
turtle.setup(width, height, startx, starty)

setup()设置窗体大小及位置
4个参数中后两个可选
setup()不是必须的

turtle 空间坐标体系

绝对坐标：以窗体为中心建立直角坐标系

turtle.goto(x, y)以（0，0）点为起点开始

import turtle
turtle.goto( 100, 100)
turtle.goto( 100,-100) 
turtle.goto(-100,-100) 
turtle.goto(-100, 100)
turtle.goto(0,0)

海龟坐标：以窗体为中心，x为前进后退方向，y为左侧右侧方向

turtle 角度坐标体系

绝对角度：极坐标的角度划分

turtle.seth(angle)
seth()改变海龟行进方向
angle为绝对度数
seth()表示只改变方向但不行

海龟角度：turtle.left angle//turtle.right angle

RGB 色彩体系-由三种颜色构成的万物色

RGB指红蓝绿三个通道的颜色组合

覆盖视力所能感知的所有颜色

RGB每色取值范围0-255整数或0-1小数

默认采用小数值可切换为整数值

1.0：RGB小数值模式
255：RGB整数值模式
1
turtle.colormode(mode)

2.4turtle程序语法元素分析

库引用与import

扩充Python 程序功能的方式

import <库名>
<库名>.<函数名>(<函数参数>)

使用from和import保留字共同完成

from <库名> import <函数名>
from <库名> import *
<函数名>(<函数参数>)

（推荐）使用import和as保留字共同完成

import <库名> as <库别名>
<库别名>.<函数名>(<函数参数>)

turtle画笔控制函数

画笔操作后一直有效，一般成对出现

turtle.penup() 别名 turtle.pu()
抬起画笔，海龟在飞行
turtle.pendown() 别名 turtle.pd()
落下画笔，海龟在爬行

画笔设置后一直有效，直至下次重新设置

turtle.pensize(width) 别名 turtle.width(width)
画笔宽度，海龟的腰围
turtle.pencolor(color) color为颜色字符串或r,g,b值
画笔颜色，海龟在涂装

pencolor(color)的 color 可以有三种形式

颜色字符串：turtle.pencolor(“purple”)
RGB的小数值：turtle.pencolor(0.63, 0.13, 0.94)
RGB的元组值：turtle.pencolor((0.63,0.13,0.94))

turtle运动控制函数

控制海龟行进：走直线 & 走曲线

turtle.forward(d) 别名 turtle.fd(d)
向前行进，海龟走直线
- d: 行进距离，可以为负数
  控制海龟行进：走直线 & 走曲线
turtle.circle(r, extent=None)
根据半径r绘制extent角度的弧形
r: 默认圆心在海龟左侧r距离的位置
extent: 绘制角度，默认是360度整圆

turtle方向控制函数

绝对角度

turtle.setheading(angle) 别名 turtle.seth(angle)
改变行进方向，海龟走角度
angle: 行进方向的绝对角度

相对角度

turtle.left(angle) 海龟向左转
turtle.right(angle) 海龟向右转
angle: 在海龟当前行进方向上旋转的角度

基本循环语句

for循环-按照一定次数循环执行一组语句

for <变量> in range(<次数>):
<被循环执行的语句>

<变量>表示每次循环的计数，0到<次数>-1

range()函数-产生循环计数序列

range(N)
产生 0 到 N-1的整数序列，共N个
range(M,N)
产生 M 到 N-1的整数序列，共N-M个

“Python蟒蛇绘制”代码分析

绘制正方形

#PythonDraw.py
import turtle as t
t.setup(650,350,200,200 )
t.penup()
t.goto(-50,-50)
t.pendown() 
t.pensize(10)
t.pencolor("black")
for i in range(4):
    t.fd(100)
    t.left(90)
t.done()

绘制六边形

#PythonDraw.py
import turtle as t
t.setup(650,350,200,200 )
t.penup()
t.right(-120)
t.fd(100)
t.pendown() 
t.pensize(5)
t.pencolor("black")
t.right(120)
for i in range(6):
    t.fd(50)
    t.left(60)
t.done()

绘制叠边形

#PythonDraw.py
import turtle as t
t.setup(650,350,200,200 )
t.penup()
t.goto(-50,-50)
t.pendown() 
t.pensize(5)
t.pencolor("black")
for i in range(9):
    t.fd(50)
    t.left(80)
t.done()

风轮绘制

#PythonDraw.py
import turtle as t
t.setup(650,350,200,200 )
t.pensize(5)
t.pencolor("black")
t.seth(-135)
for i in range(4):
    t.fd(150)
    t.left(90)
    t.circle(150,45)
    t.left(90)
    t.fd(150)
    t.right(135)
t.done()

第三章：基本数据类型

3.1数字类型及操作

整数类型

与数学中整数的概念一致

可正可负，没有取值范围限制
pow(x,y)函数：计算 xy，想算多大算多大

4种进制表示形式

十进制：1010, 99, -217
二进制，以0b或0B开头：0b010, -0B101
八进制，以0o或0O开头：0o123, -0O456
十六进制，以0x或0X开头：0x9a, -0X89

浮点数类型

与数学中实数的概念一致

带有小数点及小数的数字
浮点数取值范围和小数精度都存在限制，但常规计算可忽略
取值范围数量级约-10^307至10^308，精度数量级10^-16

浮点数间运算存在不确定尾数，不是bug

53位二进制表示小数部分,转换为十进制会出现误差

二进制表示小数，可以无限接近，但不完全相同

round(x, d)：对x四舍五入，d是小数截取位数
浮点数间运算与比较用round()函数辅助
不确定尾数一般发生在10-16左右，round()十分有效

浮点数可以采用科学计数法表示

使用字母e或E作为幂的符号，以10为基数

复数类型

与数学中复数的概念一致

z.real 获得实部

z.imag 获得虚部

数值运算操作符

加减乘除整数除，模运算（求余），幂运算（x ** y）

二元操作符有对应的增强赋值操作符

类型间可进行混合运算，生成结果为”最宽”类型

三种类型存在一种逐渐”扩展”或”变宽”的关系：
整数 -> 浮点数 -> 复数
例如：123 + 4.0 = 127.0 (整数+浮点数 = 浮点数)

数值运算函数

一些以函数形式提供的数值运算功能

abs(x)

divmod(x,y)

pow(x, y[, z])

幂余，(x**y)%z，[..]表示参数z可省略
pow(3, pow(3, 99), 10000) 结果为 4587

3.2实例3: 天天向上的力量

问题1： 1‰的力量

#DayDayUpQ1.py 
dayup = pow(1.001, 365) 
daydown = pow(0.999, 365) 
print("向上：{:.2f}，向下：{:.2f}".format(dayup, daydown))

问题3：工作日的力量

#DayDayUpQ3.py
dayup = 1.0
dayfactor = 0.01
for i in range(365):
if i % 7 in [6,0]:
dayup = dayup*(1-dayfactor)
else:
dayup = dayup*(1+dayfactor)
print("工作日的力量：{:.2f} ".format(dayup))

问题4：工作日的努力到什么水平，才能与每天努力1%一样？

def dayUP(df):
    dayup = 1
    for i in range(365):
        if i % 7 in [6,0]:
            dayup = dayup*(1 - 0.01)
        else:
            dayup = dayup*(1 + df)
    return dayup
dayfactor = 0.01
while dayUP(dayfactor) < 37.78:
    dayfactor += 0.001
print("工作日的努力参数是: {:.3f}".format(dayfactor))

3.3字符串类型及操作

3.3.1字符串：由0个或多个字符组成的有序字符序列

3.3.2字符串类型的表示

字符串有2类共4种表示方法

由一对单引号或双引号表示，仅表示单行字符串
“请输入带有符号的温度值: “ 或者 ‘C’
由一对三单引号或三双引号表示，可表示多行字符串

‘’’ Python
```
            语言   '''
```

字符串的序号：正向递增序号和反向递减序号

使用[ ]获取字符串中一个或多个字符

索引：返回字符串中单个字符 <字符串>[M]

“请输入带有符号的温度值: “[0] 或者 TempStr[-1]

切片：返回字符串中一段字符子串 <字符串>[M: N]

“请输入带有符号的温度值: “[1:3] 或者 TempStr[0:-1]

使用[M:N: K]根据步长对字符串切片

字符串的特殊字符：转义符\

“\b”回退”\n”换行(光标移动到下行首)”\r”回车(光标移动到本行首)

3.3.3字符串操作符

获取星期字符串

#WeekNamePrintV1.py
weekStr = "星期一星期二星期三星期四星期五星期六星期日"
weekId = eval(input("请输入星期数字(1-7)："))
pos = (weekId – 1 ) * 3
print(weekStr[pos: pos+3])

#WeekNamePrintV2.py
weekStr = "一二三四五六日"
weekId = eval(input("请输入星期数字(1-7)："))
print("星期" + weekStr[weekId-1])

3.3.4字符串处理函数

chr(u)：u为Unicode编码，返回其对应的字符

ord(x)：x为字符，返回其对应的Unicode编码

Unicode编码-Python字符串的编码方式

统一字符编码，即覆盖几乎所有字符的编码方式
从0到1114111 (0x10FFFF)空间，每个编码对应一个字符
Python字符串中每个字符都是Unicode编码字符
有趣尝试chr(10004)

3.3.5字符串处理方法

str.lower() 或 str.upper()	返回字符串的副本，全部字符小写/大写”AbCdEfGh”.lower() 结果为 “abcdefgh”
str.split(sep=None)	返回一个列表，由str根据sep被分隔的部分组成”A,B,C”.split(“,”) 结果为 [‘A’,’B’,’C’]
str.count(sub)	返回子串sub在str中出现的次数”an apple a day”.count(“a”) 结果为 4
str.replace(old, new)	返回字符串str副本，所有old子串被替换为new “python”.replace(“n”,”n123.io”) 结果为”python123.io”
str.center(width[,fillchar])	字符串str根据宽度width居中，fillchar可选”python”.center(20,”=”) 结果为 ‘=======python=======’

3.3.6字符串类型的格式化

<模板字符串>.format(<逗号分隔的参数>)

槽内部对格式化的配置方式

{ <参数序号> ： <格式控制标记>}

：	<填充>	<对齐>	<宽度>	<,>	<.精度>	<类型>
引导符号	用于填充的单个字符	< 左对齐 > 右对齐 ^ 居中对齐	槽设定的输出宽度	数字的千位分隔符	浮点数小数精度或字符串最大输出长度	整数类型 b, c, d, o, x, X 浮点数类型 e, E, f, %

3.4time库基本介绍

概述：time库是Python中处理时间的标准库

计算机时间的表达
提供获取系统时间并格式化输出功能
提供系统级精确计时功能，用于程序性能分析

time库包括三类函数

时间获取：time() ctime() gmtime()
时间格式化：strftime() strptime()
程序计时：sleep(), perf_counter()

时间获取

函数	描述
time()	获取当前时间戳，即计算机内部时间值，浮点数 >>>time.time() 1516939876.6022282
ctime()	获取当前时间并以易读方式表示，返回字符串 >>>time.ctime() ‘Fri Jan 26 12:11:16 2018’
gmtime()	获取当前时间，表示为计算机可处理的时间格式 >>>time.gmtime() time.struct_time(tm_year=2018, tm_mon=1, tm_mday=26, tm_hour=4, tm_min=11, tm_sec=16, tm_wday=4, tm_yday=26, tm_isdst=0)

时间格式化-将时间以合理的方式展示出来

格式化：类似字符串格式化，需要有展示模板
展示模板由特定的格式化控制符组成

strftime()方法

函数	方法
strftime(tpl,ts)	tpl是格式化模板字符串，用来定义输出效果 ts是计算机内部时间类型变量 >>>t = time.gmtime() >>>time.strftime(“%Y-%m-%d %H:%M:%S”,t) ‘2018-01-26 12:55:20’

%Y-年份/%m-月份/%d-日期

%H-小时/%P-上下午/%S-秒

程序计时应用

程序计时应用广泛

程序计时指测量起止动作所经历时间的过程
测量时间：perf_counter()
产生时间：sleep()

函数	描述
sleep（）	s拟休眠的时间，单位是秒，可以是浮点数 >>>def wait(): time.sleep(3.3) >>>wait() #程序将等待3.3秒后再退出
perf_counter()	返回一个CPU级别的精确时间计数值，单位为秒由于这个计数值起点不确定，连续调用差值才有意义 >>>start = time.perf_counter() 318.66599499718114 >>>end = time.perf_counter() 341.3905185375658 >>>end - start 22.724523540384666

3.5实例4：文本进度条

初级版本

#TextProBarV1.py
import time 
scale = 10
print("------执行开始------")
for i in range(scale+1): 
	a = '*' * i
	b = '.' * (scale - i) 
	c = (i/scale)*100
	print("{:^3.0f}%[{}->{}]".format(c,a,b)) time.sleep(0.1)
print("------执行结束------")

“文本进度条”单行动态刷新\r

刷新的本质是：用之后打印的字符覆盖之前的字符
不能换行：print()需要被控制
要能回退：打印后光标退回到之前的位置 \r

#TextProBarV2.py
import time
for i in range(101): 
    print("\r{:3}%".format(i), end="")
	time.sleep(0.1)

完整代码

#TextProBarV3.py
import time 
scale = 50
print("执行开始".center(scale//2, "-"))
start = time.perf_counter()
for i in range(scale+1): 
    a = '*' * i
	b = '.' * (scale - i) 
    c = (i/scale)*100
	dur = time.perf_counter() - start
	print("\r{:^3.0f}%[{}->{}]{:.2f}s".format(c,a,b,dur),end='') 			       time.sleep(0.1)
print("\n"+"执行结束".center(scale//2,'-'))

计算问题扩展

文本进度条程序使用了perf_counter()计时
计时方法适合各类需要统计时间的计算问题
例如：比较不同算法时间、统计程序运行时间
PY01B15 天志

文本进度条的不同设计函数

设计名称	设计函数
Liner	f(x) = x
early pause	f(x) = x+(1-sin(xπ2+π/2)/-8
late pause	f(x) = x+(1-sin(xπ2+π/2)/8
solw wavy	f(x) = x+sin(xπ5)/20
fast wavy	f(x) = x+sin(xπ20)/80
power	f(x) = (x+(1-x)*0.03)^2
inverse power	f(x) =1+(1-x)^1.5 *-1
fast power	f(x) = (x+(1-x)/2)^8
inver fast power	f(x) = 1+(1-x)^3 *-1

第三单元作业-凯撒密码

s = input()
t = ""
for c in s:
    if 'a' <= c <= 'z': 
        t += chr( ord('a') + ((ord(c)-ord('a')) + 3 )%26 )
    elif 'A' <= c <= 'Z':
        t += chr( ord('A') + ((ord(c)-ord('A')) + 3 )%26 )
    else:
        t += c
print(t)

第四章：程序控制结构

4.1程序的分支结构

单分支结构：根据判断条件结果而选择不同向前路径的运行方式

if <条件> :
<语句块>

二分支结构：根据判断条件结果而选择不同向前路径的运行方式

if <条件> :
<语句块1>
else :
<语句块2>

紧凑形式：适用于简单表达式的二分支结构

<表达式1> if <条件> else <表达式2>

多分支结构

if <条件1> :
<语句块1>
elif <条件2> :
<语句块2>
……
else :
<语句块N>

注意多条件之间的包含关系
注意变量取值范围的覆盖

条件判断及组合

判断语句

“<”“<=”“=”“!=”“==”

条件组合：用于条件组合的三个保留字

操作符及使用	描述
x and y	两个条件x和y的逻辑与
x or y	两个条件x和y的逻辑或
not x	条件x的逻辑非

程序的异常处理

错误提示的三个点：异常代码发生的代码行数，异常类型，异常内容提示

try :
<语句块1>
except :
<语句块2>

try :
<语句块1>
except <异常类型> :
<语句块2>

异常处理的高级使用

try :
<语句块1>
except :
<语句块2>
else :
<语句块3>
finally :
<语句块4>

finally对应语句块4一定执行
else对应语句块3在不发生异常时执行

4.2实例5：身体质量指数BMI

国际BMI

#CalBMIv1.py
height, weight = eval(input("请输入身高(米)和体重(公斤)[逗号隔开]: "))
bmi = weight / pow(height, 2)
print("BMI 数值为：{:.2f}".format(bmi))
who = ""
if bmi < 18.5:
    who = "偏瘦"
elif 18.5 <= bmi < 25:
    who = "正常"
elif 25 <= bmi < 30:
    who = "偏胖"
else:
    who = "肥胖"
print("BMI 指标为:国际'{0}'".format(who))

国内国际BMI

#CalBMIv3.py
height, weight = eval(input("请输入身高(米)和体重(公斤)[逗号隔开]: "))
bmi = weight / pow(height, 2)
print("BMI 数值为：{:.2f}".format(bmi))
who, nat = "", ""
if bmi < 18.5:
    who, nat = "偏瘦", "偏瘦"
elif 18.5 <= bmi < 24:
    who, nat = "正常", "正常"
elif 24 <= bmi < 25:
    who, nat = "正常", "偏胖"
elif 25 <= bmi < 28:
    who, nat = "偏胖", "偏胖"
elif 28 <= bmi < 30:
    who, nat = "偏胖", "肥胖"
else:
    who, nat = "肥胖", "肥胖"
print("BMI 指标为:国际'{0}', 国内'{1}'".format(who, nat))

4.3程序的循坏结构

遍历循环：遍历某个结构形成的循环运行方式

for <循环变量> in <遍历结构> :
<语句块>

从遍历结构中逐一提取元素，放在循环变量中
由保留字for和in组成，完整遍历所有元素后结束
每次循环，所获得元素放入循环变量，并执行一次语句块

应用1：计数循环(特定次)———-熟悉range()函数的性质

for i in range(M,N,K) :
<语句块>

应用2：字符串遍历循环

for c in s :
<语句块>

s是字符串，遍历字符串每个字符，产生循环

应用3：列表遍历循环

for item in ls :
<语句块>

ls是一个列表，遍历其每个元素，产生循环

for item in [123, “PY”, 456] :
print(item, end=”,”)

应用4：文件遍历循环

for line in fi :
<语句块>

fi是一个文件标识符，遍历其每行，产生循环

for line in fi :
print(line)

无限循环：由条件控制的循环运行方式

while <条件> :
<语句块>

反复执行语句块，直到条件不满足时结束

循环控制保留字：break 和continue

break跳出并结束当前整个循环，执行循环后的语句
continue结束当次循环，继续执行后续次数循环
break和continue可以与for和while循环搭配使用

循环的高级用法

for <变量> in <遍历结构> :
<语句块1>
else :
<语句块2>

while <条件> :
<语句块1>
else :
<语句块2>

当循环没有被break语句退出时，执行else语句块
else语句块作为**”正常”完成循环的奖励**
这里else的用法与异常处理中else用法相似

4.4模块3：random库的使用

random库基本介绍

概述：random库是使用随机数的Python标准库

伪随机数: 采用梅森旋转算法生成的(伪)随机序列中元素
random库主要用于生成随机数
使用random库: import random

random库包括两类函数，常用共8个

基本随机数函数： seed(), random()
扩展随机数函数： randint(), getrandbits(), uniform(),
randrange(), choice(), shuffle()

基本随机数函数

函数	描述
seed(a=None)	初始化给定的随机数种子，默认（如果你不给他赋初值）为当前系统时间 >>>random.seed(10) #产生种子10对应的序列
random()	生成一个[0.0, 1.0)之间的随机小数 >>>random.random() 0.5714025946899135

扩展随机数函数

函数	描述
randint(a, b)	生成一个[a, b]之间的整数 >>>random.randint(10, 100) 64
randrange(m, n[, k])	生成一个[m, n)之间以k为步长的随机整数 >>>random.randrange(10, 100, 10) 80
getrandbits(k)	生成一个k比特长的随机整数 >>>random.getrandbits(16) 37885
uniform(a, b)	生成一个[a, b]之间的随机小数 >>>random.uniform(10, 100) 13.096321648808136
choice(seq)	从序列seq中随机选择一个元素 >>>random.choice([1,2,3,4,5,6,7,8,9]) 8
shuffle(seq)	将序列seq中元素随机排列，返回打乱后的序列 >>>s=[1,2,3,4,5,6,7,8,9];random.shuffle(s);print(s) [3, 5, 8, 9, 6, 1, 2, 7, 4]

4.5实例6：圆周率的计算

公式法

#CalPiV1.py
pi = 0
N = 100
for k in range(N):
    pi += 1/pow(16,k)*( \
              4/(8*k+1) - 2/(8*k+4) - \
              1/(8*k+5) - 1/(8*k+6) ) 
print("圆周率值是: {}".format(pi))

蒙特卡罗方法

#CalPiV2.py
from random import random
from time import per_counter
DARTS = 1000*1000
hits = 0.0
start = perf_counter()
for i in range(1，DARTS+1)：
	x,y = random(),random()
    dist = pow(x **2 + y ** 2,0.5)
    if dist <=1.0:
        hits = hits +1
pi = 4 * (hits/DARTS)
print("圆周率值是：{}".format(pi))
print("运行时间是：{:.5f}s".format(perf_counter()-start))

4.6练习

一点思考

在练习中，我发现一个很有意思的错误

题目任然是蒙特卡洛计算圆周率，请以123作为随机数种子，获得用户输入的撒点数量，编写程序输出圆周率的值，保留小数点后6位。输入：1024；输出：3.218750

#CalPiV2.py
import random
DARTS = eval(input())
random.seed(123)
hits = 0.0
for i in range(DARTS+1):
    x, y = random.random(), random.random()
    dist = pow(x ** 2 + y ** 2, 0.5)
    if dist <= 1.0:
        hits = hits + 1
pi = 4 * (hits/DARTS)
print("{:.6f}".format(pi))

在输入为1048576时，结果是错误的

#CalPiV2.py
import random
DARTS = eval(input())
random.seed(123)
hits = 0.0
for i in range(1, DARTS+1):
    x, y = random.random(), random.random()
    dist = pow(x ** 2 + y ** 2, 0.5)
    if dist <= 1.0:
        hits = hits + 1
pi = 4 * (hits/DARTS)
print("{:.6f}".format(pi))

这就是成功的，那么为什么整数循环控制出了问题呢？？？显然可以改成range(DARTS)

通过这个例子，我认识到了range()函数的控制范围，程序必须严谨。

水仙花数

例如：ABC是一个”3位水仙花数”，则：A的3次方＋B的3次方＋C的3次方 = ABC。‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬

请按照从小到大的顺序输出所有的3位水仙花数，请用”逗号”分隔输出结果。

关键在于把数字和字符串怎么联系起来？你细品

s = ""
for i in range(100, 1000):
    t = str(i)
    if pow(eval(t[0]),3) + pow(eval(t[1]),3) + pow(eval(t[2]),3) == i :
        s += "{},".format(i)
print(s[:-1])

用户登录的三次机会–涉及到计数问题时，无限循环非常好用

#ThreeChancesOfUserToAssign.py
count = 0
while count < 3:
    name = input()
    password = input()
    if name == 'Kate'and password == '666666':
        print("登录成功！")
        break
    else:
        count += 1
        if count == 3:
            print("3次用户名或者密码均有误！退出程序。")

四位玫瑰数

for i in range(1000, 10000):
    t = str(i)
    if pow(eval(t[0]),4) + pow(eval(t[1]),4) + pow(eval(t[2]),4) + pow(eval(t[3]),4)== i :
        print(i)

100以内素数之和

num = 0
cond = 0
for i in range(2,101):
    for j in range(2,i):
        if i%j == 0:
            cond = 1
            break
    if cond == 0:
        num += i
    else:
        cond = 0
print(num)

第五章：函数和代码复用

函数式编程主要源于C语言，Python不是C，”函数式编程”的说法不流行，Python编程中函数不必须，因此更灵活，更探寻本质

5.1 函数的定义与使用

5.1.1函数的理解与定义

函数是一段代码的表示（下面是废话）

函数是一段具有特定功能的、可重用的语句组
函数是一种功能的抽象，一般函数表达特定功能
两个作用：降低编程难度和代码复用

5.1.2函数的使用及调用过程—调用是运行函数代码的方式

调用时要给出实际参数
实际参数替换定义中的参数
函数调用后得到返回值

5.1.3函数的参数传递

参数个数：函数可以有参数，也可以没有，但必须保留括号

def <函数名>() :
<函数体>
return <返回值>

可选参数传递：函数定义时可以为某些参数指定默认值，构成可选参数

注意：可选必须在非可选后面

def <函数名>(<非可选参数>, <可选参数>) :
<函数体>
return <返回值>

可变参数传递：函数定义时可以设计可变数量参数，即不确定参数总数量

def <函数名>(<参数>, *b ) :
<函数体>
return <返回值>

参数传递的两种方式：函数调用时，参数可以按照位置或名称方式传递

5.1.4函数的返回值-函数可以返回0个或多个结果

return保留字用来传递返回值
函数可以有返回值，也可以没有，可以有return，也可以没有
return可以传递0个返回值，也可以传递任意多个返回值

5.1.5局部变量和全局变量-使用规则

组合数据类型在python中是由指针来体现的，如果函数中没有真实创建组合数据类型，它使用的变量是使用的指针。

基本数据类型，无论是否重名，局部变量与全局变量不同
可以通过global保留字在函数内部声明全局变量
组合数据类型，如果局部变量未真实创建，则是全局变量

5.1.6lambda函数—lambda函数返回函数名作为结果

lambda函数是一种匿名函数，即没有名字的函数
使用lambda保留字定义，函数名是返回结果
lambda函数用于定义简单的、能够在一行内表示的函数

<函数名> = lambda <参数>: <表达式>

》》》f = lambdax, y : x + y

》》》f = lambda: “lambda函数”

谨慎使用lambda函数

lambda函数主要用作一些特定函数或方法的参数
lambda函数有一些固定使用方式，建议逐步掌握
一般情况，建议使用def定义的普通函数

5.2 实例7: 七段数码管绘制

步骤1：绘制单个数字对应的数码管

七段数码管由7个基本线条组成
七段数码管可以有固定顺序
不同数字显示不同的线条
增加七段数码管之间线条间隔

步骤2：获得一串数字，绘制对应的数码管

步骤3：获得当前系统时间，绘制对应的数码管

使用time库获得系统当前时间
增加年月日标记
年月日颜色不同

应用问题的扩展

绘制带小数点的七段数码管
带刷新的时间倒计时效果
绘制高级的数码管

#SevenDigitsDrawV1.py
import turtle
def drawLine(draw):   #绘制单段数码管
    turtle.pendown() if draw else turtle.penup()
    turtle.fd(40)
    turtle.right(90)
def drawDigit(digit): #根据数字绘制七段数码管
    drawLine(True) if digit in [2,3,4,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,3,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,6,8] else drawLine(False)
    turtle.left(90)
    drawLine(True) if digit in [0,4,5,6,8,9] else drawLine(False)
    drawLine(True) if digit in [0,2,3,5,6,7,8,9] else drawLine(False)
    drawLine(True) if digit in [0,1,2,3,4,7,8,9] else drawLine(False)
    turtle.left(180)
    turtle.penup()#为绘制后续数字确定位置
    turtle.fd(20) #为绘制后续数字确定位置
def drawDate(date):  #获得要输出的数字
    for i in date:
        drawDigit(eval(i))  #通过eval()函数将数字变为整数
def main():
    turtle.setup(800, 350, 200, 200)
    turtle.penup()
    turtle.fd(-300)
    turtle.pensize(5)
    drawDate('20181010')
    turtle.hideturtle()
    turtle.done()
main()

完全版

#SevenDigitsDrawV2.py
import turtle, time
def drawGap(): #绘制数码管间隔
    turtle.penup()
    turtle.fd(5)
def drawLine(draw):   #绘制单段数码管
    drawGap()
    turtle.pendown() if draw else turtle.penup()
    turtle.fd(40)
    drawGap()
    turtle.right(90)
def drawDigit(d): #根据数字绘制七段数码管
    drawLine(True) if d in [2,3,4,5,6,8,9] else drawLine(False)
    drawLine(True) if d in [0,1,3,4,5,6,7,8,9] else drawLine(False)
    drawLine(True) if d in [0,2,3,5,6,8,9] else drawLine(False)
    drawLine(True) if d in [0,2,6,8] else drawLine(False)
    turtle.left(90)
    drawLine(True) if d in [0,4,5,6,8,9] else drawLine(False)
    drawLine(True) if d in [0,2,3,5,6,7,8,9] else drawLine(False)
    drawLine(True) if d in [0,1,2,3,4,7,8,9] else drawLine(False)
    turtle.left(180)
    turtle.penup()
    turtle.fd(20)
def drawDate(date):
    turtle.pencolor("red")
    for i in date:
        if i == '-':
            turtle.write('年',font=("Arial", 18, "normal"))
            turtle.pencolor("green")
            turtle.fd(40)
        elif i == '=':
            turtle.write('月',font=("Arial", 18, "normal"))
            turtle.pencolor("blue")
            turtle.fd(40)
        elif i == '+':
            turtle.write('日',font=("Arial", 18, "normal"))
        else:
            drawDigit(eval(i))
def main():
    turtle.setup(800, 350, 200, 200)
    turtle.penup()
    turtle.fd(-350)
    turtle.pensize(5)
#    drawDate('2018-10=10+')
    drawDate(time.strftime('%Y-%m=%d+',time.gmtime()))
    turtle.hideturtle()
    turtle.done()
main()

5.3 代码复用与函数递归

函数和对象是实现代码复用的方法，也可以说是对代码抽象的不同级别

函数的递归本质就是（数学归纳法）两条，通过研究第n步与第n-1步的关系，并不关心问题具体的结构。

5.3.1代码复用与模块化设计

5.3.1.1函数和对象是实现代码复用的方法，也可以说是对代码抽象的不同级别

1函数：将代码命名在代码层面建立了初步抽象

2对象：属性和方法. 和.()，在函数之上再次组织进行抽象

5.3..1.2模块化设计-分而治之

通过函数或对象封装将程序划分为模块及模块间的表达

具体包括：主程序、子程序和子程序间关系

分而治之：一种分而治之、分层抽象、体系化的设计思想

模块内部紧耦合、模块之间松耦合

5.3.2函数递归-函数定义中调用函数自身的方式
5.3.2.1两个关键特征

1链条：计算过程存在递归链条

2基例：存在一个或多个不需要再次递归的基例

总结：递归是数学归纳法思维的编程体现

5.3.2.2函数递归的调用过程–函数+ 分支语句

递归本身是一个函数，需要函数定义方式描述

函数内部，采用分支语句对输入参数进行判断

基例和链条，分别编写对应代码

注意：递归不提高程序执行效率。//任何递归程序都可以通过堆栈或队列变成非递归程序（这是程序的高级应用）。
5.3.2.3函数递归实例解析
1将字符串s反转后输出
1
2
3
4
5
def rvs(s):
if s == "":
return s
else :
return rvs(s[1:])+s[0]

2斐波那契数列
1
2
3
4
5
def f(n):
if n ==1 or n ==2:
return 1
else:
return f(n-1)+f(n-2)

3汉诺塔问题
1
2
3
4
5
6
7
8
9
10
11
count = 0
def hanoi(n, src, dst, mid):
global count
if n== 1 :
print("{}:{}->{}".format(1,src,dst))
count+= 1
else:
hanoi(n-1, src, mid, dst)
print("{}:{}->{}".format(n,src,dst))
count += 1
hanoi(n-1, mid, dst, src)

5.4 模块4: PyInstaller库的使用
5.4.1PyInstaller库基本介绍-将.py源代码转换成无需源代码的可执行文件
PyInstaller库的安装

(cmd命令行) pip install pyinstaller

5.4.2PyInstaller库使用说明
简单的使用

(cmd命令行) pyinstaller -F <文件名.py>

PyInstaller库常用参数

参数描述

-h 查看帮助

–clean 清理打包过程中的临时文件

-D,–onedir 默认值，生成dist文件夹

-F,–onefile 在dist文件夹中只生成独立的打包文件

-i<图标文件名.ico> 指定打包程序使用的图标(icon)文件

使用：pyinstaller–icurve.ico –F SevenDigitsDrawV2.py

5.5 实例8: 科赫雪花小包裹
科赫曲线的绘制

递归思想：函数+分支

递归链条：线段的组合

递归基例：初始线段

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#KochDrawV1.py
import turtle
def koch(size, n):
if n == 0:
turtle.fd(size)
else:
for angle in [0, 60, -120, 60]:
turtle.left(angle)
koch(size/3, n-1)
def main():
turtle.setup(800,400)
turtle.penup()
turtle.goto(-300, -50)
turtle.pendown()
turtle.pensize(2)
koch(600, 3) # 3阶科赫曲线，阶数
turtle.hideturtle()
main()

科赫雪花的绘制–对三角形每一条边进行分形
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#KochDrawV2.py
import turtle
def koch(size, n): #绘制科赫曲线的每一个长度size，和阶数n
if n == 0:
turtle.fd(size)
else:
for angle in [0, 60, -120, 60]:
turtle.left(angle)
koch(size/3, n-1)
def main():
turtle.setup(600,600)
turtle.penup()
turtle.goto(-200, 100)
turtle.pendown()
turtle.pensize(2)
level = 3 # 3阶科赫雪花，阶数
koch(400, level)
turtle.right(120)
koch(400, level)
turtle.right(120)
koch(400, level)
turtle.hideturtle()
main()

对编写后的科赫雪花代码进行打包处理

pyinstaller –i curve.ico –F KochDrawV2.py

“科赫雪花小包裹”举一反三
绘制条件的扩展

修改分形几何绘制阶数

修改科赫曲线的基本定义及旋转角度

修改绘制科赫雪花的基础框架图形

分形几何千千万

康托尔集、谢尔宾斯基三角形、门格海绵…

龙形曲线、空间填充曲线、科赫曲线…

函数递归的深入应用…

练习题中的思考
例1——-任意累积：计算任意个输入数字的乘积。
1
2
3
4
5
6
7
# 官方的答案.py
def cmul(a ,*b) # 无限制数量函数定义的方法，体现在可变参数传递上
m = a
for i in b
m*= i
return m
print(eval("cuml([])".format(input())))

官方是把输入当作多个变量来使用，我的思维是把输入当成一个变量来看。回想可变参数就是允许在调用参数的时候传入多个（≥0个）参数（类似于列表、字典），我的参数定义方法虽然使用上和列表没有区别，单数参数接收到的是一个tuple（这些参数在传入时被自动组组装为一个元祖），你细品（笑）

1
2
3
4
5
6
def cmul(*s):
results = 1
for i in s:
results *= i
return results
print(eval("cmul({})".format(input())))

例2———–连续质数计算
获得用户输入数字N，计算并输出从N开始的5个质数，单行输出，质数间用逗号,分割。‪‬‪‬‪‬‪‬‪‬‮‬‫‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‪‬‪‬‮‬‫‬‮‬

要求：需要考虑用户输入的数字N可能是浮点数，应对输入取整数；最后一个输出后不用逗号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def prime(m):
if m < 2:
return False
else:
end = int(pow(m, 0.5) + 1)
for i in range(2, end):
if m%i == 0:
return False
else:
return True

n = eval(input())
if n != int(n): # 因为可能输入有浮点数
n = int(n) + 1
else: # 保证输入5.0时，输出为整数5。这里只根据题目中只输入正浮点或者正整数时做的处理
n = int(n)
count = 5
while count > 0:
if prime(n):
if count > 1:
print(n, end=',')
else:
print(n)
count -= 1
n += 1

计数用什么来着？（经典）质数是怎么判断的？

下文接（二）