Weakly Supervised Discriminative Feature Learning with State Information
论文展示
论文代码
论文阅读
每个行人图片都会有视角、姿态等状态信息，虽然自身不带标签，但可以预测这些状态信息作为伪标签，
摘要
我们建立了一个简单的伪标签模型，并利用状态信息通过弱监督决策边界校正和弱监督特征漂移正则化来改进分配的伪标签。
由于无监督学习通常存在结果出错的问题，一些未标签的样本会偏离正确的决策边界，为此作者提出了弱监督决策边界修正（weakly supervised decision boundary rectification）来解决这个问题，由此每个样本获得了一个伪类，作为状态信息。
当特征失真严重时，样本会偏移到不正确的决策区域，但每个状态都有着特定的失真模式，会使得样本产生特定的偏移，对此作者提出了弱监督特征漂移正则化（weakly supervised feature drift regularization）。
背景
论文主体结构
基于状态信息的弱监督判别学习
设$$ \mathbf{U} = {u_{i}}{i=1}^N $$表示未标记的训练集，其中$${u{i}}$$是一个未标记的图像示例。我们还知道状态 $$ s{i} \in {1,\cdots,\mathbf{J} } ,u_{i}$$的照明是dark, normal还是bright。我们的目标是学习一个深度网络$$ f $$来提取识别特征，其表示为$$ x = f(u;\theta) $$。
每个特征特征向量 x 都属于一个代理类（surrogate class）$$\mu$$，
判别学习问题定义为：
$$\min_{\theta,{\mu_{k}}} L_{surr} = -\sum_{x}log \frac{exp(x^{T}\mu_{\hat{y}})}{\sum_{k=1}^{K}exp(x^{T}\mu_{k})} $$
其中 $$K$$ 表示代理类的数量，$$ \hat{y}$$表示$$ x $$的代理类的标签，即$$\hat{y} = \arg\max_{k} {exp(x^{T}\mu{k})} $$,
并且$$ \hat{y}$$ 是动态更新的量。
推导：$$x$$为第$$y$$类的概率值为：$$ p(x \mid y) = \frac{exp(- {\parallel x-\mu_{y} \parallel}^2/2)}{\sum_{k=1}^{K}exp(- {\parallel x-\mu_{y} \parallel}^2/2)}$$
设置：$$ {\parallel x \parallel}{2} = 1,{\parallel \mu{k} \parallel}_{2} = 1$$
则$$ - {\parallel x-\mu_{y} \parallel}^2/2 = x^{T}\mu_{y} + 1$$
概率值更新为：$$ p(x \mid y) = \frac{exp(x^{T}\mu_{\hat{y}})}{\sum_{k=1}^{K}exp(x^{T}\mu_{k})}$$
弱监督决策边界修正
量化一个代理类被状态支配的程度，称为 Maximum Predominance Index（MPI），表示为在代理类中最常见状态的比例。第 k 个代理类的MPI定义为：
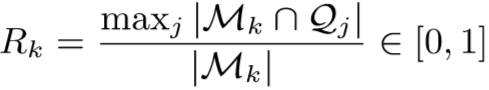
其中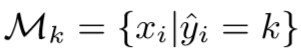
，
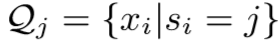，则分母表示为该代理类的元素数量，分子表示为代理类中最常见状态的元素数量，
会动态更新。
Rk 越高，表明一些样本错误的进入了代理类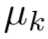
中（直观理解，每个代理类，即每个行人被不同监控拍摄下来，所包含的状态分布相对均匀）。由此得到弱监督的修正分配为：
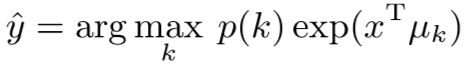
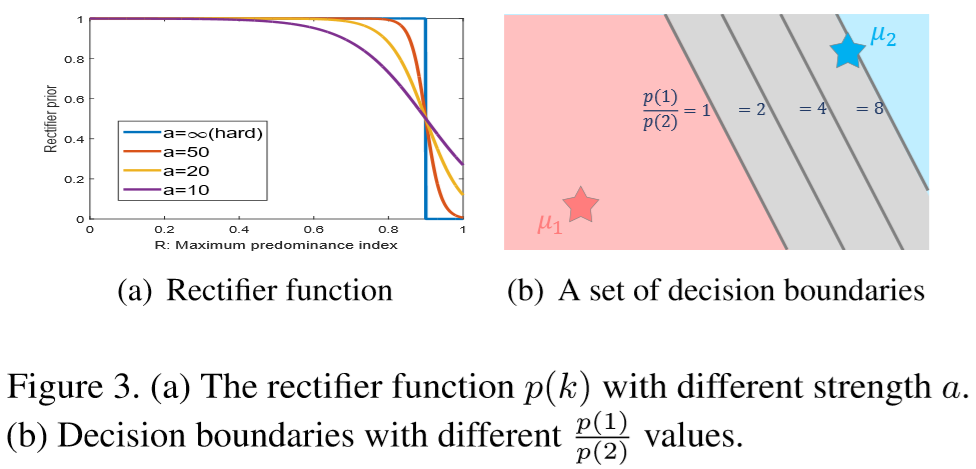
其中 p(k) 为修正函数，用于抑制 Rk 较高的代理类，具体为：
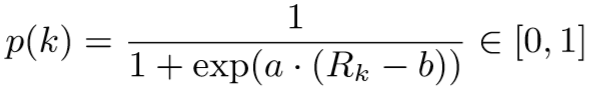
上述称为 soft rectifier 函数，若 b = 0.95， a = 无穷，可以简化得到 hard rectifier 函数：
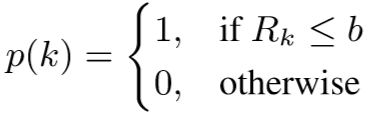
对于 hard rectifier 函数，当超过阈值时，比如这部分决策区域超过95%的样本都是黑暗的，那么说明这部分过于黑无法匹配出行人，则取消这片决策区域；
对于 soft rectifier 函数，当超过阈值时，决策区域不会无效，而是对决策边界进行调整。
二分类的决策边界推导：
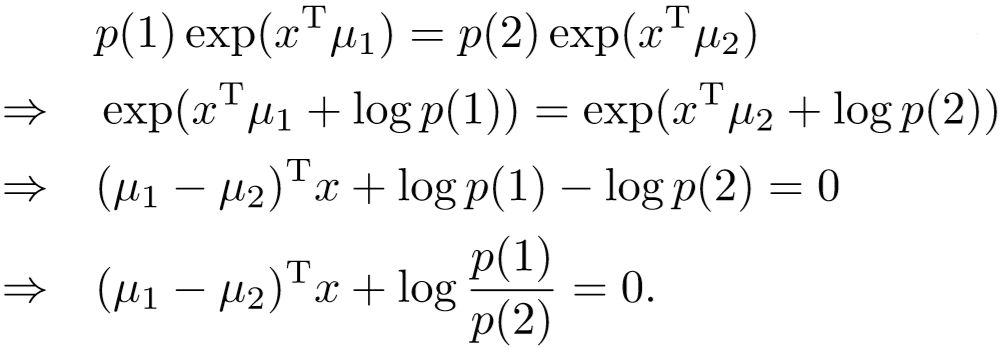
弱监督特征漂移正则化
视觉的主导状态会导致显著的特征失真，但其遵循着特定的失真模式，比如低分率状态下颜色暗淡、纹理模糊等。定义状态子分布（state sub-distribution）为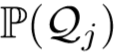
，所有未标签的训练集的分布为
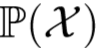，其中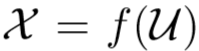
，特征失真会导致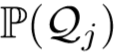远离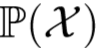，作者提出校准子分布和总分布，来对抗特征的漂移，即 WFDR：
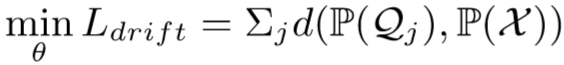
其中 d 为Wasserstein距离，衡量两个分布之间的距离【传送门】，为了计算的方便，对距离计算进行简化：
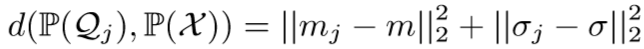
其中 
分别为
中特征向量的均值和方差，
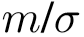分别为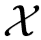
中特征向量的均值和方差。
（3）结合两方面的考虑，得到总损失函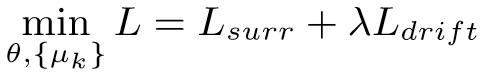
主干网络采用ResNet-50，训练迭代次数为1600次，batchsize = 384，momentum = 0.9，weight decay = 0.005，采用梯度下降法，学习率为0.001，并在1000、1400次迭代后下降至0.1倍。
实验experiment
将模型应用到两个领域进行测试：行人重识别和姿态鲁棒人脸识别：
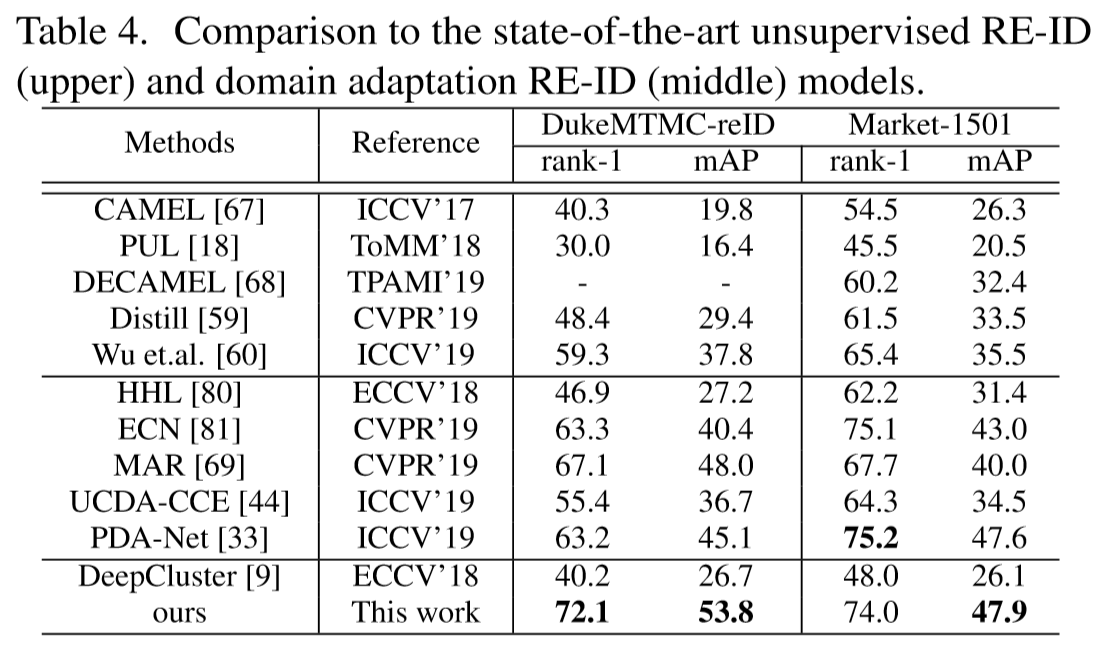
- 行人重识别
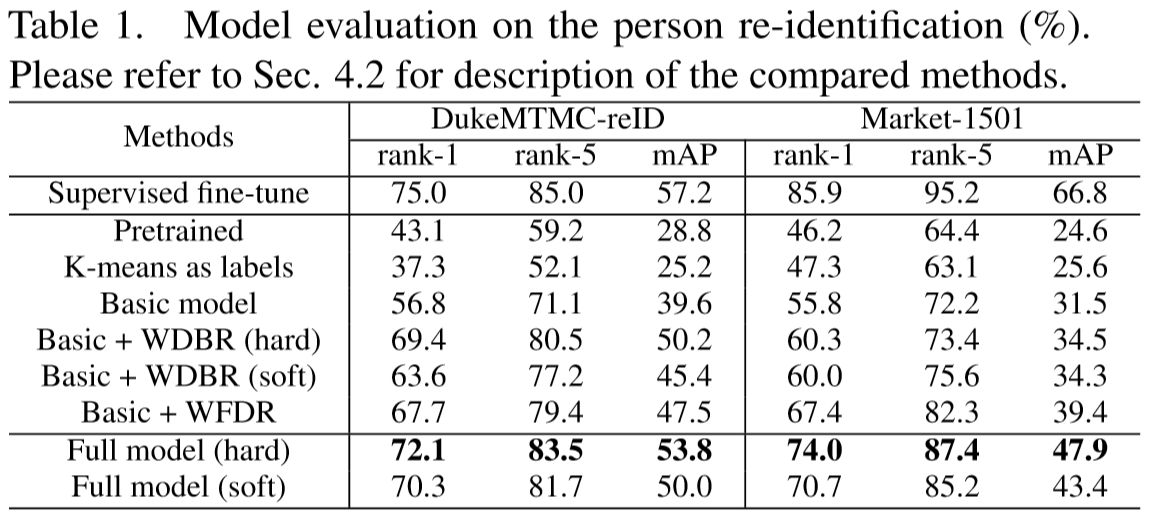
- 姿态鲁棒人脸识别
Rectifier (neural networks) - 整流函数
在人工神经网络的背景下，线性整流器是一个激活函数，被定义为其参数的正数部分：
$$ f(x) = x^{+} = max (0,x)$$
在神经网络中，线性整流作为神经元的激活函数，定义了该神经元在线性变换 $$\mathbf {w} ^{T}\mathbf {x} + b$$ 之后的非线性输出结果。对于进入神经元的来自上一层神经网络的输入向量$$ x $$，使用线性整流激活函数的神经元会输出
$$max(0,\mathbf {w} ^{T}\mathbf {x} + b)$$
至下一层神经元或作为整个神经网络的输出 (取决现神经元在网络结构中所处位置)。
实际运行时 batchsize = 384
Batch Size定义：一次训练所选取的样本数。
为什么要提出Batch Size？
在没有使用Batch Size之前，这意味着网络在训练时，是一次把所有的数据（整个数据库）输入网络中，然后计算它们的梯度进行反向传播，由于在计算梯度时使用了整个数据库，所以计算得到的梯度方向更为准确。但在这情况下，计算得到不同梯度值差别巨大，难以使用一个全局的学习率，所以这时一般使用Rprop这种基于梯度符号的训练算法，单独进行梯度更新。
Epoch（时期）：
当一个完整的数据集通过了神经网络一次并且返回了一次，这个过程称为一次>epoch。（也就是说，所有训练样本在神经网络中都* 进行了一次正向传播* 和一次反向传播* ）
再通俗一点，一个Epoch就是*将所有训练样本训练一次**的过程。然而，当一个Epoch的样本（也就是所有的训练样本）数量可能太过庞大（对于计算机而言），就需要把它分成多个小块，也就是就是分成*多个Batch 来进行训练。*
Batch（批 / 一批样本）：
将整个训练样本分成若干个Batch。Batch_Size（批大小）：
每批样本的大小。Iteration（一次迭代）：
训练一个Batch就是一次Iteration（这个概念跟程序语言中的迭代器相似）。
